算法设计复习指南
算法设计复习指南
考核方式
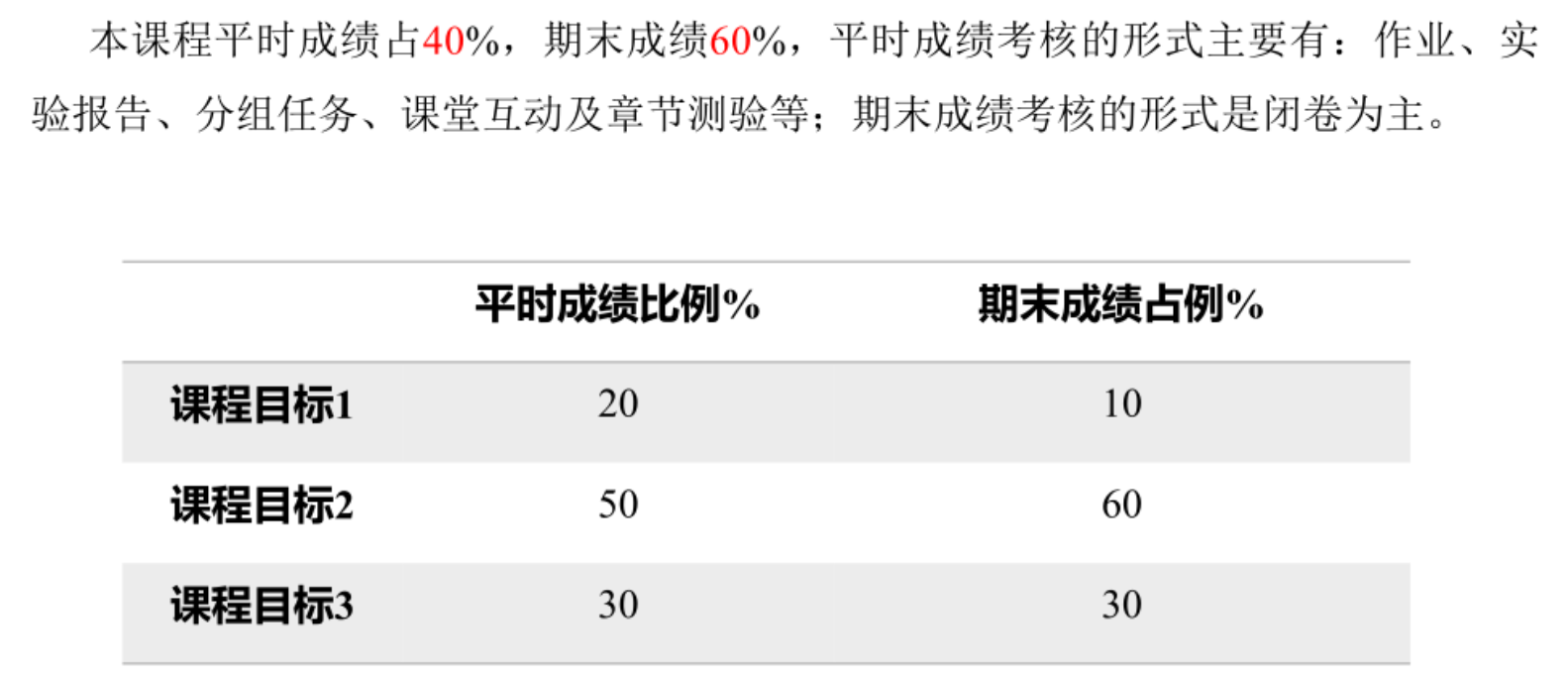

课程目标

主要章节与核心知识点
第一章 算法基础


- 算法复杂度分析

- 时间复杂度与空间复杂度的定义
- 渐近符号:O(上界)、Ω(下界)、θ(紧界)
- 常数因子不影响渐近复杂度
- 常见复杂度比较:O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(2ⁿ) < O(n!)
算法设计基本概念
- 算法的五大特性:输入、输出、有穷性、确定性、可行性
- 算法设计的目标:正确性、可读性、健壮性、效率(时间+空间)
常见算法复杂度
复杂度 典型算法示例 O(1) 数组访问 O(logn) 二分查找 O(n) 线性搜索 O(nlogn) 快速排序、归并排序 O(n²) 冒泡排序、选择排序、直接插入排序 O(n³) 矩阵乘法(朴素算法) O(2ⁿ) 递归斐波那契 O(n!) 全排列 说明:
- 直接插入排序:最好情况O(n)(数组已排序),平均和最坏情况O(n²)
- 快速排序:平均情况O(nlogn),最坏情况O(n²)(数组已排序或逆序)
第二章 分治法
分治法的基本要素
- 分解:将原问题分解为若干规模较小、结构相似的子问题
- 解决:递归解决子问题,或直接解决小规模子问题
- 合并:将子问题的解合并为原问题的解
分治法适用条件
- 子问题结构与原问题相似
- 子问题相互独立(无重叠子问题)
- 子问题的解可以合并
典型应用
- 二分查找
- 快速排序
- 归并排序
- 大整数乘法
- 矩阵乘法(Strassen算法)
- 寻找第k小元素
递归
定义:递归是一种解决问题的方法,它将原问题分解为规模更小的相同问题,通过不断调用自身来解决子问题,直到问题规模小到可以直接解决。
基本思想:
- 将复杂问题分解为简单的子问题
- 子问题与原问题具有相同的结构
- 解决子问题后,将结果合并得到原问题的解
递归要素:
- 终止条件(边界条件):当问题规模足够小时,可以直接返回结果,不再继续递归
- 递归调用(递归方程):将原问题分解为更小的子问题,调用自身函数
- 返回值处理:将子问题的结果合并,得到原问题的解
递归与迭代的比较:
- 递归:代码简洁,但空间复杂度高,可能栈溢出
- 迭代:效率更高,空间复杂度低,但代码可能更复杂
第三章 贪心算法
贪心算法的基本思想
- 每一步选择局部最优解,希望通过局部最优达到全局最优
- 贪心准则(最优度量标准): 贪心法每一步上用作决策依据的选择标准
- 贪心选择性质:全局最优解可以通过一系列局部最优选择得到
- 最优子结构性质:问题的最优解包含其子问题的最优解
贪心算法的要素
- 贪心选择性质
- 最优子结构性质
典型应用
- 活动安排问题
- 哈夫曼编码
- 单源最短路径(Dijkstra算法)
- 基本思想:采用贪心策略,每次选择当前距离源点最近的未访问节点,更新其邻接节点的距离
- 适用场景:带非负权重的有向图或无向图,求解从一个源点到所有其他顶点的最短路径
- 时间复杂度:使用优先队列优化时为O(E log V),其中V是顶点数,E是边数
- 工作流程:初始化距离数组→迭代选择最小距离节点→更新邻接节点距离→重复直到所有节点访问完成
- 最小生成树(Prim算法、Kruskal算法)
- Prim算法:
- 基本思想:从一个顶点开始,每次添加一条连接生成树和外部顶点的最小权重边
- 适用场景:稠密图,边数较多的连通加权无向图
- 时间复杂度:使用优先队列优化时为O(E log V)
- 工作流程:初始化顶点集合→迭代选择最小边→扩展生成树→重复直到包含所有顶点
- Kruskal算法:
- 基本思想:按边权从小到大排序,每次添加不形成环的最小边
- 适用场景:稀疏图,边数较少的连通加权无向图
- 时间复杂度:O(E log E)(主要来自边的排序)
- 工作流程:排序所有边→使用并查集检测环→依次添加边→直到生成树形成
- Prim算法:
- 背包问题(分数背包)
贪心算法与动态规划的区别
算法 搜索策略 子问题处理 适用场景 贪心算法 自顶向下 每次选择局部最优 具有贪心选择性质 动态规划 自底向上 解决重叠子问题 子问题重叠
第四章 回溯法
回溯法的基本思想
- 系统地搜索问题的所有解
- 采用深度优先搜索策略,通过剪枝避免无效搜索
- 解空间树:子集树(0-1选择)、排列树(排列问题)

回溯法的关键技术
- 剪枝函数:约束函数(可行性剪枝)、限界函数(最优性剪枝)
- 解空间的组织与遍历
典型应用
- 0-1背包问题
- 旅行商问题
- n皇后问题
- 图的着色问题
- 子集和问题
时间复杂度分析

变量/术语的含义如下:
x[k]:回溯法会把问题的解表示为一个“解向量”(比如
x[1],x[2],…,x[n]),x[k]就是这个向量的第k个元素,对应“第k步选择的选项”(比如八皇后问题中,x[k]表示第k行皇后放在第几个列)。显约束:是对
x[k]的“基本限制”(比如八皇后问题中,x[k]必须是1~8的整数,不能超出棋盘范围),满足显约束的x[k]才是“合法的候选选项”。约束函数(constraint):是“隐约束”的判断函数,用来筛选掉不符合问题规则的
x[k](比如八皇后问题中,constraint会判断当前选的x[k]是否和之前的皇后冲突)。上界函数(bound):用于“剪枝”的函数,判断当前路径即使继续选下去,也不可能得到更优解(比如背包问题中,
bound会计算当前物品+剩余物品的最大价值,若小于已有最优解就直接剪枝)。- 子集树问题:O(n×2ⁿ)
- 排列树问题:O(n×n!)
- 上界函数:用于剪枝优化,计算当前状态下可能的最大价值上限
第五章 分支限定法
分支限定法的基本思想
- 分支:将问题分解为子问题
- 限定:计算子问题的上下界,剪枝无效分支
- 采用广度优先搜索或优先队列搜索策略
分支限定法的设计
- 1.设计合适的限界函数
- 2.组织活结点表




- 3.确定最优解向量

总结
- 分支限定法与回溯法的区别
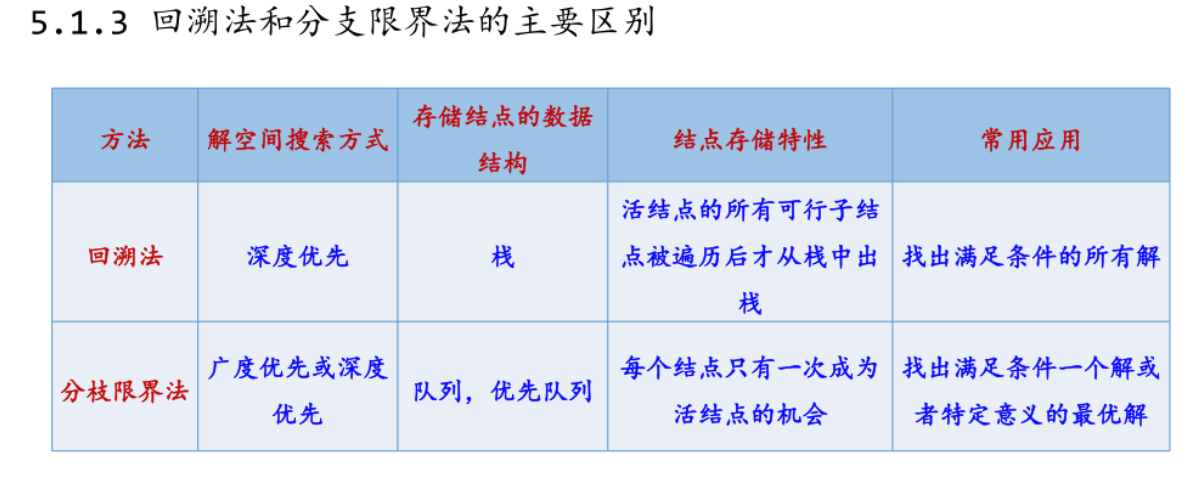
最小出边限界法
定义:分支限界法的具体实现,主要用于求解旅行商问题(TSP),采用贪心策略+下界剪枝+优先队列管理活结点。
核心思想:
- 贪心选择:每次扩展当前节点的最小出边
- 下界剪枝:计算路径下界,剪枝不可能优于当前最优解的路径
- 优先队列:按下界从小到大排列活结点,优先扩展更优路径
核心要素:
- 优先队列:管理活结点,按下界排序
- 下界函数:计算路径的最小可能总成本
- 剪枝策略:下界≥当前最优解时剪枝
下界计算(考点):
- 最小出边法:每个节点保留两条最小出边,计算剩余路径最小成本
- 最小生成树法:剩余节点的最小生成树 + 已有路径成本 + 首尾节点最小边
适用场景:旅行商问题(TSP)、路径优化问题
与分支限界法关系:是分支限界法在TSP问题上的具体应用,体现了分支限界法的核心思想(剪枝+优先队列)
分支限界法与分治法和回溯法的关系
与分治法的关系:
- 相似点:都采用“分解-求解-合并”的思想,将原问题分解为子问题
- 不同点:
- 分治法递归求解所有子问题,然后合并子问题的解;分支限界法通过限界函数剪枝,只处理可能产生最优解的子问题
- 分治法的子问题相互独立;分支限界法的子问题可能存在依赖关系
- 分治法适用于求解所有子问题的解,分支限界法适用于求解最优解
与回溯法的关系:
- 相似点:都基于问题的解空间树进行搜索,通过剪枝策略减少搜索空间
- 不同点:
- 搜索策略:回溯法采用深度优先搜索(DFS);分支限界法可采用深度优先搜索(DFS)、广度优先搜索(BFS)或优先队列搜索(最佳优先搜索)
- 搜索目标:回溯法通常求解所有满足条件的解,分支限界法主要求解最优解
- 剪枝策略:回溯法使用约束函数(可行性剪枝)和限界函数(最优性剪枝);分支限界法主要使用限界函数进行剪枝
- 存储结构:回溯法通常使用栈;分支限界法使用栈(DFS)、队列(BFS)或优先队列(最佳优先搜索)
- 效率:对于求解最优解问题,分支限界法通常比回溯法更高效
三种算法的比较:
算法 核心思想 搜索策略 适用场景 分治法 分解-递归-合并 递归 子问题独立,求解所有子问题的解 回溯法 深度优先搜索+剪枝 深度优先搜索 求解所有满足条件的解或特定解 分支限界法 分支+限界 DFS/BFS/优先队列 求解最优解问题
第六章 动态规划
动态规划的基本思想
- 将原问题分解为相互重叠的子问题,通过求解子问题来求解原问题
- 自底向上计算,保存子问题的解,避免重复计算
- 核心是找到状态转移方程
动态规划的适用条件
- 最优子结构性质:原问题的最优解包含子问题的最优解
- 重叠子问题性质:子问题重复出现,需要保存子问题的解
动态规划的基本要素
- 状态定义:描述问题的不同阶段和状态
- 状态转移方程:描述状态之间的转移关系
- 初始条件:问题的边界条件
- 计算顺序:自底向上,从小到大计算
与其他算法的比较
算法 子问题特点 搜索策略 适用场景 分治法 子问题不重叠 递归 子问题独立 贪心算法 无重叠子问题 自顶向下 具有贪心选择性质 动态规划 子问题重叠 自底向上 具有最优子结构和重叠子问题
第七章 智能算法
智能算法的基本概念
- 智能算法是一类启发式算法,模拟自然现象或生物行为
- 适用于求解复杂的组合优化问题
- 主要特点:全局搜索能力强,不依赖问题的具体结构
粒子群优化算法(PSO)
- 基本思想:模拟鸟群或鱼群的群体智能行为,通过粒子间的协作和竞争寻找最优解
- 核心概念:
- 粒子:问题的潜在解
- 粒子位置:粒子在解空间中的位置
- 粒子速度:粒子在解空间中的移动速度
- 惯性权重:决定粒子保持当前速度的程度
- 认知因子:粒子向自身历史最优位置移动的权重
- 社会因子:粒子向群体最优位置移动的权重
- 个体最优(pbest):粒子自身找到的最优解
- 全局最优(gbest):整个粒子群找到的最优解
- 适应度函数:评价粒子优劣的函数
- 终止条件:算法停止的条件(最大迭代次数或收敛)
- 算法流程:初始化粒子群 → 计算适应度 → 更新个体最优和全局最优 → 更新粒子位置和速度 → 重复迭代
- 应用领域:函数优化、神经网络训练、组合优化问题
模拟退火算法(SA)
- 基本思想:模拟固体退火过程,通过控制温度的冷却来寻找最优解
- 核心概念:
- 温度:控制搜索的随机性,温度越高,接受劣解的概率越大
- 冷却速率:控制温度下降的速度
- 邻域函数:生成当前解的邻居解
- Metropolis准则:决定是否接受劣解

- 算法流程:初始化温度和初始解 → 生成邻居解 → 计算能量差 → 按Metropolis准则接受或拒绝 → 降低温度 → 迭代直到满足终止条件
- 应用领域:旅行商问题、图着色问题、电路设计
禁忌搜索算法(TS)
- 基本思想:通过记忆机制避免重复搜索,允许接受劣解以跳出局部最优
- 核心概念:

- 禁忌表:记录最近访问过的解或操作,避免重复搜索
- 禁忌长度:禁忌表的大小,控制记忆的时间
- 候选解:当前解的邻居解
- 特赦规则:当找到更优解时,可忽略禁忌表的限制
- 算法流程:初始化当前解和禁忌表 → 生成候选解 → 选择最优候选解(考虑禁忌表) → 更新禁忌表 → 迭代直到满足终止条件
- 应用领域:旅行商问题、车间调度问题、资源分配问题
智能算法的优缺点
算法 优点 缺点 PSO 实现简单,收敛速度快 容易陷入局部最优 SA 全局搜索能力强 参数设置敏感,收敛速度慢 TS 记忆机制避免重复搜索 禁忌表长度难以确定 - 优点:全局搜索能力强,适用于复杂问题,不需要问题的梯度信息
- 缺点:收敛速度可能较慢,参数设置敏感,理论基础相对薄弱
答题技巧
贪心算法通用模板(Prim / Kruskal / Dijkstra)
解:本题采用贪心算法(×××算法)求解。
1. 问题建模与适用性说明:
本题满足贪心选择性质和最优子结构,因此可以采用贪心算法求解。
2. 初始化:
给出初始解集及辅助数据结构。
(如:Dijkstra 中,已确定集合 S={源点},
dist[i] 表示源点到顶点 i 的当前最短距离,并初始化相关值;
Prim 中维护已选顶点集合和最小边权数组;
Kruskal 中对所有边按权值排序并初始化并查集。)
3. 贪心选择策略:
在所有候选元素中,选择当前代价最小且满足约束条件的元素。
4. 状态更新:
将选中的元素加入解集中,并更新相关辅助信息。
5. 重复执行(迭代过程):
循环执行“选择—更新”,每一轮明确写出选择对象及更新结果,
直到满足终止条件。
6. 最终结果:
输出最优解及对应的总代价。例题:
给定下图,使用 Dijkstra 算法求从顶点 A 到其他所有顶点的最短路径。
解:采用贪心算法(Dijkstra 算法)求解。
1. 问题建模与适用性说明:
该问题是单源最短路径问题,满足贪心选择性质,适合使用 Dijkstra 算法。
2. 初始化:
- 已确定顶点集合 S={A}
- 距离数组 dist 初始化:
dist[A]=0,dist[B]=∞,dist[C]=2,dist[D]=5,dist[E]=3,dist[F]=∞
3. 第1轮贪心选择:
从 S 外选择 dist 最小的顶点 C(2)。
4. 第1轮状态更新:
- S={A,C}
- 更新:
dist[B]=4,dist[D]=3
5. 重复执行(完整迭代过程):
- 第2轮:选 D(3),S={A,C,D},检查邻接点,dist 无变化
- 第3轮:选 E(3),S={A,C,D,E},更新 dist[F]=7
- 第4轮:选 B(4),S={A,B,C,D,E},dist 无变化
- 第5轮:选 F(7),S={A,B,C,D,E,F},算法结束
6. 最终结果:
A→B=4,A→C=2,A→D=3,A→E=3,A→F=7动态规划通用模板(必考重点)
解:采用动态规划方法。
1. 状态定义:
明确 dp 的含义,并结合问题说明其实际意义。
2. 状态转移方程:
根据问题条件给出状态转移关系,并解释转移原因。
3. 初始条件:
给出边界状态的取值及含义。
4. 计算顺序与迭代过程:
说明 dp 表的填表顺序,并展示关键迭代过程。
5. 最终结果:
指出题目所求答案对应的 dp 状态。例题:给定字符串 s1="ABCBDAB",s2="BDCAB",求最长公共子序列长度。
解:采用动态规划方法。
1. 状态定义:
dp[i][j] 表示 s1 前 i 个字符与 s2 前 j 个字符的 LCS 长度。
2. 状态转移方程:
- s1[i-1]==s2[j-1]:dp[i][j]=dp[i-1][j-1]+1
- 否则:dp[i][j]=max(dp[i-1][j], dp[i][j-1])
3. 初始条件:
dp[0][j]=0,dp[i][0]=0。
4. 计算顺序与迭代过程:
按行填表:
- i=1:依次计算 dp[1][1]~dp[1][5]
- i=2:依次计算 dp[2][1]~dp[2][5]
- …
每一步均由左方与上方状态递推得到。
5. 最终结果:
dp[7][5]=4。分治算法模板(快速排序、归并、最近点对)
解:采用分治算法。
1. 问题分解:
将原问题划分为若干规模更小、结构相同的子问题。
2. 递归求解:
递归求解每个子问题,并写出递归展开过程。
3. 合并结果:
将子问题的解逐层合并。
4. 递归终止条件:
子问题规模为 1 或可直接求解时返回。例题:使用归并排序对数组 [38,27,43,3,9,82,10] 排序。
解:采用分治算法(归并排序)求解。
1. 问题分解:
[38,27,43,3,9,82,10]
→ [38,27,43] 与 [3,9,82,10]
→ [38,27] 与 [43], [3,9] 与 [82,10]
→ 直到子数组长度为 1。
2. 递归求解:
子数组长度为 1 时视为已有序。
3. 合并结果:
- [38] 与 [27] → [27,38]
- [27,38] 与 [43] → [27,38,43]
- [3] 与 [9] → [3,9]
- [82] 与 [10] → [10,82]
- 最终合并得到有序数组。
4. 递归终止条件:
子数组长度为 1。
最终结果:[3,9,10,27,38,43,82]回溯算法模板(N 皇后、全排列、子集)
解:采用回溯算法。
1. 状态表示:
定义搜索状态及其含义。
2. 搜索扩展:
在当前状态下按顺序尝试所有可能选择。
3. 约束判断与剪枝:
若当前状态违反约束,则立即回溯。
4. 解的判定与记录:
当达到目标状态时记录解。
5. 回溯过程:
说明递归进入与返回的过程。
6. 最终结果:
输出所有合法解或最优解。例题:求解 4 皇后问题。
解:采用回溯算法求解。
1. 状态表示:
x[i] 表示第 i 行皇后所在列。
2. 搜索扩展:
第1行依次尝试列1~4。
3. 约束判断与剪枝:
若与已放置皇后同列或同对角线,则剪枝。
4. 回溯过程示例:
- 第1行放2 → 第2行放4 → 第3行放1 → 第4行放3,得到解
- 回溯至第3行,尝试其他列,若冲突则继续回溯
5. 解的判定与记录:
成功放置第4个皇后时记录解。
6. 最终结果:
共 2 个解:[2,4,1,3],[3,1,4,2]分支限界算法模板(TSP、0-1 背包)
解:采用分支限界法求解。
1. 解空间建模:
将问题表示为解空间树,节点为部分解。
2. 界限计算:
为每个节点计算上下界。
3. 节点选择策略:
优先扩展界限最优节点。
4. 剪枝条件:
界限不优于当前最优解则剪枝。
5. 搜索迭代过程:
按节点扩展顺序给出搜索过程。
6. 最终结果:
输出最优解。例题:使用分支限界法求解 4 城市 TSP。
解:采用分支限界法求解。
1. 解空间建模:
节点表示当前路径及路径长度。
2. 界限计算:
下界 = 当前路径 + 剩余城市最小出边和。
3. 搜索迭代过程:
- 初始节点 A
- 扩展 A→B、A→C、A→D
- 选择下界最小节点继续扩展
- 形成完整回路并更新最优解
4. 剪枝条件:
下界 ≥ 当前最优值时剪枝。
5. 最终结果:
最优路径 A→B→C→D→A,总长度 26。搜索算法模板(BFS / DFS)
解:采用(BFS / DFS)搜索算法。
1. 状态与数据结构定义:
定义搜索状态及队列/栈或递归结构。
2. 初始化:
起点入队或作为递归起点。
3. 搜索过程:
通过循环或递归不断扩展状态。
4. 终止条件与结果:
达到目标状态时结束搜索。例题:使用 BFS 求解迷宫最短路径问题。
解:采用 BFS 搜索算法。
1. 状态定义:
状态为 (x,y,dist)。
2. 初始化:
起点入队,dist=0,标记访问。
3. 搜索过程(循环):
- 出队一个位置
- 向四个方向扩展合法位置
- 新位置入队并更新距离
4. 终止条件与结果:
首次到达终点即停止。
最终结果:最短路径长度为 8。示例
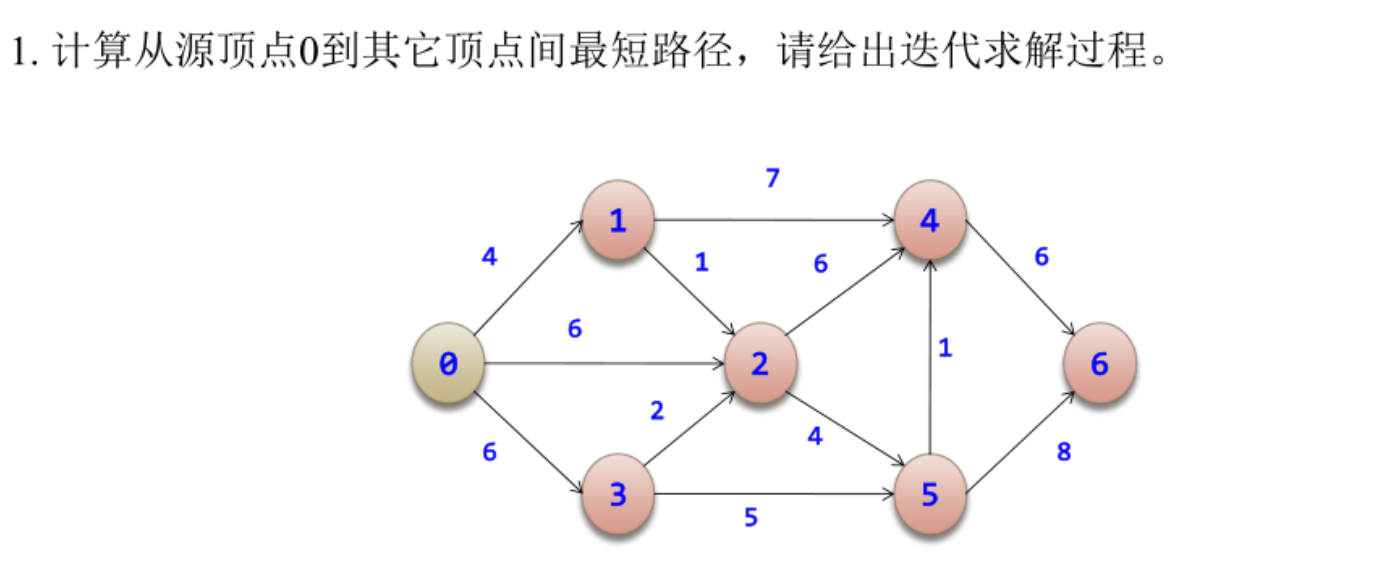
解:本题采用 Dijkstra 算法求从源点 0 到其余各顶点的最短路径。
1. 问题建模与适用性说明
本题为单源最短路径问题,图中各边权值均为非负数,满足最优子结构和贪心选择性质,适合采用 Dijkstra 算法求解。
2. 初始化
设 S 为已确定最短路径的顶点集合,dist[i] 表示从源点 0 到顶点 i 的当前最短距离。
初始时:
S = {0}
dist = [0, 4, 6, 6, ∞, ∞, ∞]
3. 迭代过程与状态更新
第 1 次迭代:
在未加入 S 的顶点中选取 dist 最小的顶点 1,将其加入 S。
对与顶点 1 相邻的边进行松弛:
dist[2] = min(6, 4 + 1) = 5
dist[4] = min(∞, 4 + 7) = 11
更新后:
dist = [0, 4, 5, 6, 11, ∞, ∞]
第 2 次迭代:
选取 dist 最小的未确定顶点 2,加入 S。
松弛相关边:
dist[5] = min(∞, 5 + 4) = 9
更新后:
dist = [0, 4, 5, 6, 11, 9, ∞]
第 3 次迭代:
选取顶点 3,加入 S。
对其相邻边进行松弛后,dist 不发生变化。
第 4 次迭代:
选取顶点 5,加入 S。
松弛操作:
dist[4] = min(11, 9 + 1) = 10
dist[6] = min(∞, 9 + 8) = 17
更新后:
dist = [0, 4, 5, 6, 10, 9, 17]
第 5 次迭代:
选取顶点 4,加入 S。
松弛操作:
dist[6] = min(17, 10 + 6) = 16
第 6 次迭代:
选取顶点 6,加入 S,所有顶点均已确定,算法结束。
4. 最终结果
从源点 0 到其余各顶点的最短路径长度为:
0→1 = 4,0→2 = 5,0→3 = 6,0→5 = 9,0→4 = 10,0→6 = 16