课中习题

第二章 分治法

k选择

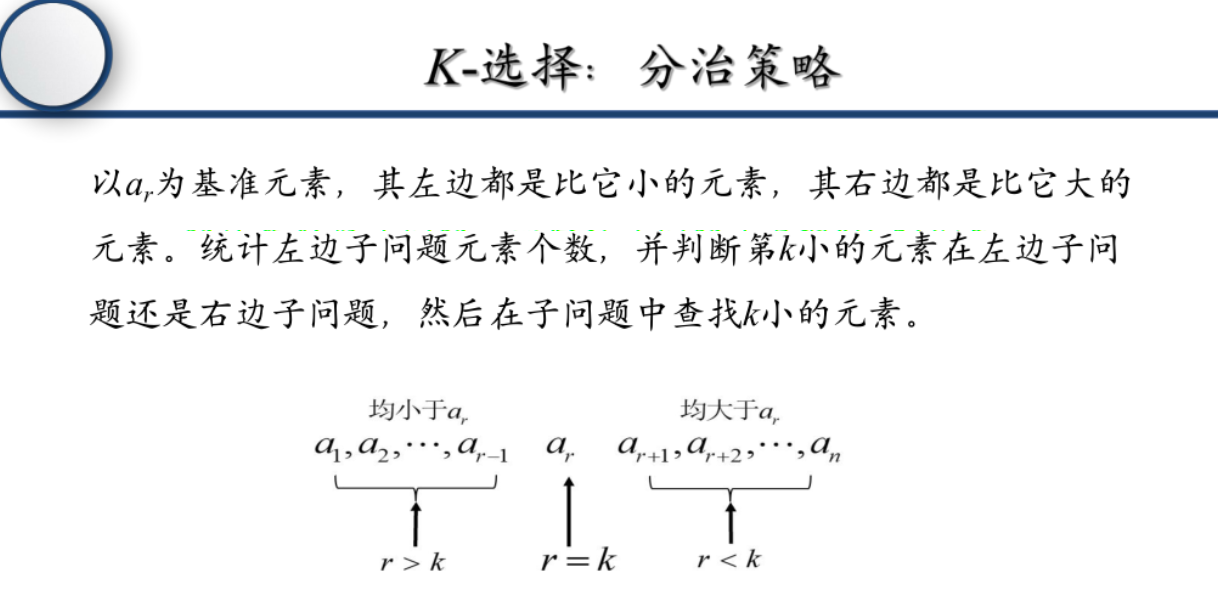
核心思路：
使用分治法求解k选择问题（找到第k小元素），基于快速排序的思想，通过分区操作减少搜索范围。

分治法模板应用：

1. 问题建模与适用性说明：

   • 问题：在无序数组中找到第k小的元素
   • 适用性：分治法适合此类问题，因为可以通过分区操作将问题规模减半，平均时间复杂度为O(n)

2. 算法设计：

   • 分解：使用快速排序的分区函数，选择一个基准元素，将数组分为两部分，左边元素都小于等于基准，右边元素都大于等于基准
   • 递归求解：根据基准元素的位置与k的关系，选择继续在左半部分或右半部分查找
   • 合并结果：当基准元素的位置等于k时，直接返回该元素

3. 算法步骤：

   • 选择基准元素，对数组进行分区
   • 计算基准元素在数组中的位置pos
   • 若pos == k-1（假设k从1开始），返回基准元素
   • 若pos > k-1，在左半部分递归查找第k小元素
   • 若pos < k-1，在右半部分递归查找第k-pos-1小元素

4. 时间复杂度分析：

   • 平均时间复杂度：O(n)
   • 最坏时间复杂度：O(n²)（当每次选择的基准都是最大或最小元素时）
   • 空间复杂度：O(log n)（递归调用栈的深度）

示例应用：

• 数组：[3, 1, 4, 1, 5, 9, 2, 6]
• 查找第3小元素：
  • 第一次分区：基准=6，left=[3,1,4,1,5,2]，right=[9]，pos=6
  • 由于6 > 2（k-1=2），在左半部分查找
  • 左半部分继续分区，最终找到第3小元素为3

第四章 回溯法

子集和问题

核心思路：
用回溯法枚举所有可能的子集，同时通过剪枝减少无效搜索：

1. 每个元素有“选”或“不选”两种选择；
2. 剪枝条件：
   • 若当前子集和 > 目标W，直接剪枝；
   • 若当前子集和 + 剩余元素的总和 < W，直接剪枝（即使选完剩余元素也达不到W）。

子集、子序列、子数组的核心区别：

概念	定义	顺序要求	连续性要求	示例（原数组[1,2,3]）	严格差异示例
子集	原集合中元素的任意组合	无（可重新排列）	无	[]、[1]、[2]、[3]、[1,2]、[1,3]、[2,3]、[1,2,3]	理论上允许[3,1,2]（重新排列）
子序列	原序列中元素顺序不变的任意组合	有（必须保持原顺序）	无	[]、[1]、[2]、[3]、[1,2]、[1,3]、[2,3]、[1,2,3]	不允许[3,1,2]（顺序错误）
子数组	原数组中连续的一段	有（保持原顺序）	有	[1]、[2]、[3]、[1,2]、[2,3]、[1,2,3]	不允许[1,3]（不连续）

算法步骤（以示例w=[11,13,24,7], W=31为例）：

1. 排序：先将数组排序（方便剪枝，示例排序后为[7,11,13,24]）；
2. 递归回溯：
   • 维护当前索引、当前子集和、当前子集；
   • 对每个元素，尝试“选”或“不选”，并检查剪枝条件；
   • 若当前子集和 == W，记录该子集。

代码实现

def subset_sum(w, W):
    w.sort()  # 排序，方便后续剪枝
    n = len(w)
    result = []  # 存储所有满足条件的子集
    total_sum = sum(w)  # 所有元素的总和，用于剪枝

    def backtrack(index, current_sum, current_subset):
        # 找到符合条件的子集
        if current_sum == W:
            result.append(current_subset.copy())
            return
        # 越界或当前和超过W，剪枝
        if index >= n or current_sum > W:
            return
        # 剪枝：当前和 + 剩余元素总和 < W，选完也达不到，直接返回
        remaining_sum = total_sum - sum(w[:index])
        if current_sum + remaining_sum < W:
            return
        
        # 选择当前元素
        current_subset.append(w[index])
        backtrack(index + 1, current_sum + w[index], current_subset)
        # 不选择当前元素（回溯）
        current_subset.pop()
        backtrack(index + 1, current_sum, current_subset)

    backtrack(0, 0, [])
    return result

第五章 分支限定

最小出边限界法

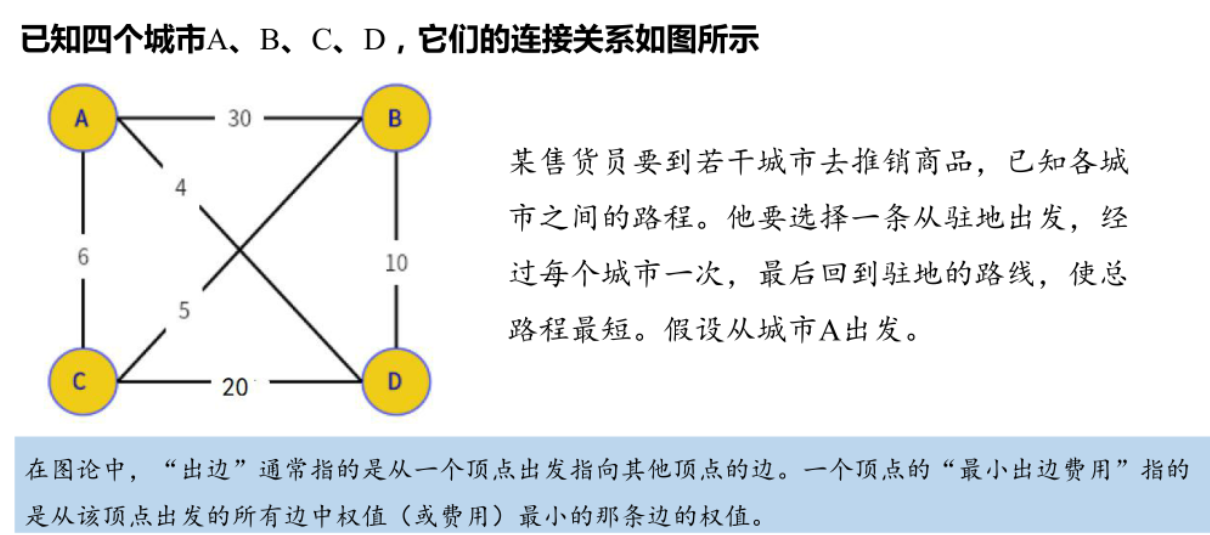
• 城市编号：A(0), B(1), C(2), D(3)
• 邻接矩阵（路径长度，∞表示无直接边）：

  graph = [
      [∞, 30, 6, 4],    # A(0)的出边：A→B(30)、A→C(6)、A→D(4)
      [30, ∞, 5, 10],   # B(1)的出边：B→A(30)、B→C(5)、B→D(10)
      [6, 5, ∞, 20],    # C(2)的出边：C→A(6)、C→B(5)、C→D(20)
      [4, 10, 20, ∞]    # D(3)的出边：D→A(4)、D→B(10)、D→C(20)
  ]

• 目标：找路径0 → v1 → v2 → v3 → 0（每个城市仅访问一次），总长度最小。

分支限定法核心逻辑：

1. 分支：以“当前路径”为节点，枚举下一个未访问的城市，生成子节点（分支）。
2. 限定（下界计算）：对每个节点，计算“当前路径长度 + 剩余城市的最小出边费用 + 回到起点的最小边费用”，若下界≥已有最优解，则剪枝（无需继续探索该分支）。
3. 优先队列：用优先队列（最小堆）存储待探索的节点，优先选择下界最小的节点（贪心策略，加速找到最优解）。

预处理：各城市的最小出边费用（用于计算下界）：

• A的最小出边：min(30,6,4) = 4
• B的最小出边：min(30,5,10) = 5
• C的最小出边：min(6,5,20) = 5
• D的最小出边：min(4,10,20) = 4

分支限定法核心代码：

import heapq

INF = float('inf')
graph = [
    [INF, 30, 6, 4],    # A(0)
    [30, INF, 5, 10],   # B(1)
    [6, 5, INF, 20],    # C(2)
    [4, 10, 20, INF]    # D(3)
]
n = 4
min_out_edge = [4, 5, 5, 4]
best_cost = INF
best_path = []

# 初始化优先队列
heap = []
heapq.heappush(heap, (sum(min_out_edge), 0, 0, frozenset([0]), [0]))

while heap:
    current_lower, current_cost, current_city, visited, path = heapq.heappop(heap)
    
    # 剪枝
    if current_lower >= best_cost:
        continue
    
    # 终止条件：访问所有城市，返回起点
    if len(visited) == n:
        total = current_cost + graph[current_city][0]
        if total < best_cost:
            best_cost = total
            best_path = path + [0]
        continue
    
    # 分支：枚举下一个城市
    for next_city in range(n):
        if next_city not in visited and graph[current_city][next_city] != INF:
            new_visited = frozenset(visited | {next_city})
            new_cost = current_cost + graph[current_city][next_city]
            
            # 计算新下界
            remaining_min = sum(min_out_edge[i] for i in range(n) if i not in new_visited)
            back_to_start = min(graph[next_city][0] for i in range(n) if graph[next_city][i] != INF)
            new_lower = new_cost + remaining_min + back_to_start
            
            if new_lower < best_cost:
                heapq.heappush(heap, (new_lower, new_cost, next_city, new_visited, path + [next_city]))

第六章 动态规划

数塔问题

数塔问题

1. 填空答案：j <= i
2. 原因：数塔第$i$层有$i$个节点，$j$的取值范围是1到$i$，故循环条件为j <= i。
3. 最大路径计算（$n=5$）：
   • 数塔数据：[[13], [11, 8], [12, 7, 26], [6, 14, 15, 8], [12, 7, 13, 24, 11]]
   • 从底层向上递推dp数组：
     • 第5层：[12, 7, 13, 24, 11]
     • 第4层：[18, 27, 39, 32]（每个元素为下一层相邻两数最大值加当前层值）
     • 第3层：[39, 46, 65]
     • 第2层：[57, 73]
     • 第1层：[86]
   • 最终最大路径值：$\boxed{86}$，路径：13 → 8 → 26 → 15 → 24

小超人追赶上司领导

小超人每步可以走1米、2米或3米，它与上司的距离为n米。请设计动态规划方案，计算小超人走n米的所有走法数量。

1. 状态定义：设dp[i]表示小超人走i米的走法总数。

2. 状态转移方程：要到达i米处，最后一步的选择为“走1米”“走2米”“走3米”，因此：

   $$dp[i] = dp[i-1] + dp[i-2] + dp[i-3]$$

3. 边界处理：

   • 当i-1 < 0时，dp[i-1]=0
   • 当i-2 < 0时，dp[i-2]=0
   • 当i-3 < 0时，dp[i-3]=0

4. 初始条件：

   • dp[0] = 1：走0米的走法是“原地不动”，共1种
   • dp[1] = 1：走1米的走法是“走1米”，共1种
   • dp[2] = 2：走2米的走法是“1+1”“2”，共2种

5. 循环处理：

   • 从第3个台阶开始循环，直到第n个台阶
   • 对于每个i（3 ≤ i ≤ n），使用状态转移方程计算dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
   • 循环过程中自动处理边界情况（通过初始条件和状态转移方程的设计）

6. 递推示例（以n=5为例）：

   • dp[3] = dp[2] + dp[1] + dp[0] = 2 + 1 + 1 = 4
   • dp[4] = dp[3] + dp[2] + dp[1] = 4 + 2 + 1 = 7
   • dp[5] = dp[4] + dp[3] + dp[2] = 7 + 4 + 2 = 13

7. 复杂度：

   • 时间复杂度：$O(n)$（遍历1到n即可完成递推）
   • 空间复杂度：$O(n)$（用数组存储dp）；可优化为$O(1)$（仅维护前3个状态的变量）

矩形数塔-1

矩形数塔-1

1. 问题解析：

   • 矩阵规模：$m=6$行，$n=7$列（$n$为奇数）
   • 出发点：最后一行（第6行）的正中间列（第4列）下方
   • 移动规则：每次可向前（上一行同列）、左前方（上一行左列）、右前方（上一行右列）移动
   • 目标：求路径上的最大数字和

2. 状态定义：设dp[i][j]表示到达第$i$行第$j$列时的最大数字和

3. 状态转移方程：

   $$dp[i][j] = \max(dp[i+1][j-1], dp[i+1][j], dp[i+1][j+1]) + data[i][j]$$

4. 边界处理：

   • 当$j-1<1$时，排除$i+1,j-1$位置
   • 当$j+1>n$时，排除$i+1,j+1$位置

5. 初始条件：最后一行（第6行）的dp值等于其本身的数字，即dp[6][j] = data[6][j]

6. 矩阵数据（从第1行到第6行）：

   • 第1行：[16, 4, 3, 12, 6, 0, 3]
   • 第2行：[4, -5, 6, 7, 0, 0, 2]
   • 第3行：[6, 0, -1, -2, 3, 6, 8]
   • 第4行：[5, 3, 4, 0, 0, -2, 7]
   • 第5行：[-1, 7, 4, 0, 7, -5, 6]
   • 第6行：[0, -1, 3, 4, 12, 4, 2]

7. 循环处理：

   • 从第5行开始向上循环，直到第1行
   • 对于每行的每个元素j（1 ≤ j ≤ n），使用状态转移方程计算dp[i][j]
   • 循环过程中自动处理边界情况

8. 递推计算（从第5行到第1行）：

   • 第5行：[2, 11, 16, 12, 19, -1, 10]
   • 第4行：[16, 19, 20, 19, 19, 17, 17]
   • 第3行：[25, 20, 19, 18, 22, 25, 25]
   • 第2行：[29, 20, 26, 29, 25, 25, 27]
   • 第1行：[45, 33, 32, 41, 35, 27, 30]

9. 最终结果：第1行的最大dp值为$\boxed{45}$，即最大数字和为45

10. 复杂度分析：

    • 时间复杂度：$O(m \times n)$（需遍历m行n列的矩阵）
    • 空间复杂度：$O(m \times n)$（用二维数组存储dp）；可优化为$O(n)$（用一维数组滚动更新）

矩形数塔-2

矩形数塔-2

1. 问题核心：
   该问题是带起点约束的矩阵路径最大和问题：

   • 矩阵为6行7列，出发点“S”对应最后一行（第6行）第4列数字“4”的下方
   • 移动规则：每次可向“当前位置的上方左列、上方同列、上方右列”移动，最终到达矩阵第一行
   • 目标：求路径上的数字最大和

2. 状态定义：
   设dp[i][j]表示从出发点到达第$i$行第$j$列时的最大数字和

3. 状态转移方程：

   $$dp[i][j] = max(dp[i+1][j-1], dp[i+1][j], dp[i+1][j+1]) + data[i][j]$$

4. 边界处理：

   • 当j-1 < 1时，dp[i+1][j-1]不参与计算
   • 当j+1 > n时，dp[i+1][j+1]不参与计算
   • 出发点在第6行第4列下方，因此第6行第4列的初始值为其本身数值

5. 初始条件：

   • 最后一行（第6行）中，只有第4列有初始值，其他列初始值为负无穷（表示不可达）
   • dp[6][4] = data[6][4] = 4
   • 其他dp[6][j] = -∞（$j ≠ 4$）

6. 循环处理：

   • 从第5行开始向上循环，直到第1行
   • 对于每行的每个元素j（1 ≤ j ≤ n），使用状态转移方程计算dp[i][j]
   • 循环过程中自动处理边界情况和不可达状态

7. 递推计算：

   • 从第5行开始向上递推，直到第1行
   • 最终取第1行中的最大值作为结果

8. 结论：
   通过动态规划计算，该矩阵从出发点到第一行的最大数字和为$\boxed{41}$

9. 复杂度分析：

   • 时间复杂度：$O(m \times n)$（需遍历m行n列的矩阵）
   • 空间复杂度：$O(m \times n)$（用二维数组存储dp）；可优化为$O(n)$（用一维数组滚动更新）

机器人爬台阶

机器人爬台阶，一次可以爬1个台阶、2个台阶、3个台阶，请计算机器人爬n个台阶有多少种爬法？

1. 状态定义：设dp[i]表示机器人爬i个台阶的爬法总数

2. 状态转移方程：

   $$dp[i] = dp[i-1] + dp[i-2] + dp[i-3]$$

3. 边界处理：

   • 当i-1 < 0时，dp[i-1] = 0
   • 当i-2 < 0时，dp[i-2] = 0
   • 当i-3 < 0时，dp[i-3] = 0

4. 初始条件：

   • dp[0] = 1（爬0个台阶只有“不爬”这1种方式，作为递推基础）
   • dp[1] = 1（爬1个台阶：仅“爬1个”这1种方式）
   • dp[2] = 2（爬2个台阶：“1+1”“2”共2种方式）

5. 循环处理：

   • 从第3个台阶开始循环，直到第n个台阶
   • 对于每个i（3 ≤ i ≤ n），使用状态转移方程计算dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
   • 循环过程中自动处理边界情况

6. 示例计算（以n=5为例）：

   • dp[3] = dp[2] + dp[1] + dp[0] = 2 + 1 + 1 = 4
   • dp[4] = dp[3] + dp[2] + dp[1] = 4 + 2 + 1 = 7
   • dp[5] = dp[4] + dp[3] + dp[2] = 7 + 4 + 2 = 13

7. 结论：
   对于任意正整数n，爬n个台阶的爬法数可通过上述动态规划递推公式计算得到。

8. 复杂度分析：

   • 时间复杂度：$O(n)$（需遍历1到n进行递推）
   • 空间复杂度：$O(n)$（用数组存储dp）；可优化为$O(1)$（仅维护前3个状态）

连续子序列的最大和

给定一个长度为n的整数序列d，找出其连续子序列的最大和。例如d=[6,-1,5,4,-7]，最大子序列和为14。

1. 算法思路（Kadane算法）：

   • 状态定义：设dp[i]表示以第i个元素结尾的连续子序列的最大和
   • 状态转移方程：dp[i] = max(d[i], dp[i-1] + d[i])（若前序子序列和为正，则拼接当前元素；否则从当前元素重新开始）
   • 全局最大值：遍历过程中记录dp[i]的最大值，即为整个序列的最大子序列和

2. 初始条件：

• dp[0] = d[0]

3. 状态转移方程：

   $$dp[i] = \max(d[i], dp[i-1] + d[i])$$

4. 循环处理：

   • 从第2个元素开始循环，直到第n个元素
   • 对于每个i（1 ≤ i < n），使用状态转移方程计算dp[i] = max(d[i], dp[i-1] + d[i])
   • 循环过程中维护一个全局最大值变量，记录当前的最大子序列和

5. 示例计算（以d=[6,-1,5,4,-7]为例）：

   • dp[0] = 6，全局最大=6
   • dp[1] = max(-1, 6-1)=5，全局最大=6
   • dp[2] = max(5, 5+5)=10，全局最大=10
   • dp[3] = max(4, 10+4)=14，全局最大=14
   • dp[4] = max(-7, 14-7)=7，全局最大保持14

6. 结论：
   该序列的最大连续子序列和为14

7. 复杂度分析：

   • 时间复杂度：$O(n)$（需遍历整个序列一次）
   • 空间复杂度：$O(n)$（用数组存储dp）；可优化为$O(1)$（仅维护前一个状态和全局最大值）

最长递增子序列（LIS）

给定序列，找出其最长递增子序列（元素为原序列的一部分且保持递增顺序）。例如序列[10,9,2,5,3,7,101,18]的一个最长递增子序列是[2,3,7,101]。

1. 状态定义：
   设dp[i]表示以原序列第i个元素结尾的最长递增子序列的长度

2. 状态转移方程：

   $$dp[i] = 1 + \max_{0 \leq j < i \text{且} d[j] < d[i]} dp[j]$$

   （若不存在满足d[j] < d[i]的j，则dp[i] = 1）

3. 初始条件：
   对于每个i，dp[i]的初始值为1（每个元素自身可构成长度为1的递增子序列）

4. 循环处理：

   • 从第2个元素开始循环，直到第n个元素
   • 对于每个i（1 ≤ i < n），遍历所有j（0 ≤ j < i）
   • 对于每个j，如果d[j] < d[i]，则更新dp[i] = max(dp[i], dp[j] + 1)
   • 循环结束后，遍历整个dp数组，找出最大值

5. 示例计算（以序列[10,9,2,5,3,7,101,18]为例）：

   • dp[0] = 1（元素10）
   • dp[1] = 1（元素9，无更小的前序元素）
   • dp[2] = 1（元素2，无更小的前序元素）
   • dp[3] = 1 + dp[2] = 2（元素5，前序元素2满足条件）
   • dp[4] = 1 + dp[2] = 2（元素3，前序元素2满足条件）
   • dp[5] = 1 + max(dp[2], dp[3], dp[4]) = 1 + 2 = 3（元素7，前序元素2、5、3满足条件）
   • dp[6] = 1 + max(dp[2], dp[3], dp[4], dp[5]) = 1 + 3 = 4（元素101，前序多个元素满足条件）
   • dp[7] = 1 + max(dp[2], dp[3], dp[4], dp[5]) = 1 + 3 = 4（元素18，前序多个元素满足条件）

6. 结论：
   遍历dp数组的最大值，即为原序列的最长递增子序列长度（示例中最大值为4，对应子序列如[2,3,7,101]）。

7. 复杂度分析：

   • 时间复杂度：$O(n^2)$（嵌套循环，外层n次，内层平均n/2次）
   • 空间复杂度：$O(n)$（用数组存储dp）
   • 优化方法：使用二分查找可以将时间复杂度优化到$O(n\log n)$

最长公共子序列

给定两个序列 $a[1],\cdots,a[m]$ 和 $b[1],\cdots,b[n]$，找出它们的最长公共子序列（子序列元素在原序列中顺序一致且对应元素相等，使子序列长度最大）。

1. 状态定义：
   设 $dp[i][j]$ 表示序列 $a[1..i]$ 和 $b[1..j]$ 的最长公共子序列长度。

2. 状态转移方程：

   • 若 $a[i] = b[j]$，则 $dp[i][j] = dp[i-1][j-1] + 1$（当前元素加入公共子序列）；
   • 若 $a[i] \neq b[j]$，则 $dp[i][j] = \max(dp[i-1][j], dp[i][j-1])$（取去掉一个序列末尾元素后的最长长度）。

3. 边界处理：

   • 当 $i = 0$ 时，$dp[0][j] = 0$（序列 $a$ 为空，无公共子序列）；
   • 当 $j = 0$ 时，$dp[i][0] = 0$（序列 $b$ 为空，无公共子序列）。

4. 循环处理：

   • 外层循环遍历序列a的每个元素i（1 ≤ i ≤ m）
   • 内层循环遍历序列b的每个元素j（1 ≤ j ≤ n）
   • 对于每个i和j，根据状态转移方程计算$dp[i][j]$：
     • 若 $a[i] = b[j]$，则 $dp[i][j] = dp[i-1][j-1] + 1$
     • 否则 $dp[i][j] = \max(dp[i-1][j], dp[i][j-1])$
   • 循环结束后，$dp[m][n]$即为最长公共子序列的长度

5. 递推示例（以 $a = [1,3,4,5,6,2,7]$、$b = [3,5,6,4,9,2,7]$ 为例）：

   • $dp[1][1] = 0$（$a[1]=1 \neq b[1]=3$）；
   • $dp[2][1] = 1$（$a[2]=3 = b[1]=3$）；
   • 最终 $dp[7][7] = 5$，对应最长公共子序列为 $[3,4,6,2,7]$。

6. 复杂度分析：

   • 时间复杂度：$O(m \times n)$（需遍历两个序列的所有元素组合）；
   • 空间复杂度：$O(m \times n)$（用二维数组存储 $dp$）；可优化为 $O(\min(m,n))$（用一维数组滚动更新）。
   • 优化方法：使用滚动数组可以将空间复杂度从$O(m \times n)$优化到$O(\min(m,n))$

方阵取宝

在 $n \times m$ 的矩阵中，从左上角出发，每次只能向右或向下移动，最终从右下角走出，求能搜集到的最大宝物价值（以示例中 $3 \times 5$ 矩阵为例）。

1. 状态定义：
   设 $dp[i][j]$ 表示到达第i行第j列时，能搜集到的最大宝物价值。

2. 状态转移方程：

   • 第一行（仅能从左侧移动）：$$dp[1][j] = dp[1][j-1] + data[1][j]$$
   • 第一列（仅能从上方移动）：$$dp[i][1] = dp[i-1][1] + data[i][1]$$
   • 其他位置（取上方/左侧最大值）：$$dp[i][j] = \max(dp[i-1][j], dp[i][j-1]) + data[i][j]$$

3. 边界处理：

   • 当 $i=1$ 且 $j=1$（起点）：无前置位置，直接取矩阵本身值 $dp[1][1] = data[1][1]$；
   • 当 $i=1$ 且 $j>1$：仅能从左方来，无需考虑上方边界
   • 当 $j=1$ 且 $i>1$：仅能从上方来，无需考虑左方边界

4. 初始条件：

   • $dp[1][1] = 1$；示例矩阵左上角（第1行第1列）的宝物价值为1
   • 所有未初始化的 $dp[i][j]$ 初始值为0（仅作为计算占位）

5. 循环处理：

   • 先填充第一行：遍历 $j$ 从 $2$ 到 $5$，按第一行转移方程计算 $dp[1][j]$；
   • 再填充第一列：遍历 $i$ 从 $2$ 到 $3$，按第一列转移方程计算 $dp[i][1]$；
   • 最后填充剩余位置：遍历 $i$ 从 $2$ 到 $3$、$j$ 从 $2$ 到 $5$，按通用转移方程计算 $dp[i][j]$；

6. 递推示例（以3×5示例矩阵为例）：
   示例矩阵（行1到3，列1到5）：
   行1：$[1, 2, 9, 9, 9]$；
   行2：$[5, 3, 3, 4, 3]$；
   行3：$[1, 2, 5, 9, 5]$；

   • 第一行计算：
     $dp[1][2] = 1+2=3$；$dp[1][3] = 3+9=12$；$dp[1][4] = 12+9=21$；$dp[1][5] = 21+9=30$；
   • 第一列计算：
     $dp[2][1] = 1+5=6$；$dp[3][1] = 6+1=7$；
   • 剩余位置计算：
     $dp[2][2] = \max(3,6)+3=9$；$dp[2][3] = \max(12,9)+3=15$；$dp[2][4] = \max(21,15)+4=25$；$dp[2][5] = \max(30,25)+3=33$；
     $dp[3][2] = \max(9,7)+2=11$；$dp[3][3] = \max(15,11)+5=20$；$dp[3][4] = \max(25,20)+9=34$；$dp[3][5] = \max(33,34)+5=39$；

7. 复杂度：

   • 时间复杂度：$O(n \times m)$（遍历矩阵所有 $n \times m$ 个元素，每个元素仅计算1次）；
   • 空间复杂度：$O(n \times m)$（用二维数组存储 $dp$）；可优化为 $O(\min(n,m))$（用一维数组滚动更新，仅保留当前行/列数据）；

摘花生

在 $n \times m$ 网格的花生地中，从左上角出发，仅能向东（右）或向南（下）移动，最终从右下角走出，求最多能摘到的花生数量。

1. 状态定义：
   设 $dp[i][j]$ 表示到达第i行第j列时，累计摘到的最大花生数。

2. 状态转移方程：

   • 第一行（仅能从左侧移动）：$$dp[1][j] = dp[1][j-1] + peanuts[1][j]$$
   • 第一列（仅能从上方移动）：$$dp[i][1] = dp[i-1][1] + peanuts[i][1]$$
   • 其他位置（取上方/左侧最大值）：$$dp[i][j] = \max(dp[i-1][j], dp[i][j-1]) + peanuts[i][j]$$

3. 边界处理：

   • 当 $i=1$ 且 $j=1$（起点）：$dp[1][1] = peanuts[1][1]$；
   • 当 $i=1$ 且 $j>1$：仅依赖左侧位置，无需考虑上方边界
   • 当 $j=1$ 且 $i>1$：仅依赖上方位置，无需考虑左侧边界

4. 初始条件：

   • $dp[1][1] = peanuts[1][1]$；（起点位置的花生数）

5. 循环处理：

   • 先填充第一行：遍历 $j$ 从 $2$ 到 $m$，按第一行转移方程计算；
   • 再填充第一列：遍历 $i$ 从 $2$ 到 $n$，按第一列转移方程计算；
   • 最后填充剩余位置：遍历 $i$ 从 $2$ 到 $n$、$j$ 从 $2$ 到 $m$，按通用转移方程计算；

6. 复杂度：

   • 时间复杂度：$O(n \times m)$（遍历所有网格点）；
   • 空间复杂度：$O(n \times m)$（二维数组存储 $dp$）；可优化为 $O(\min(n,m))$（一维数组滚动更新）；

地宫取宝

在 $n \times m$ 网格的地宫宝库中，从左上角出发，仅能向右或向下移动，经过格子时可拿取“价值大于手中所有宝贝”的物品（也可选择不拿），求走到右下角时恰好持有k件宝贝的行动方案数。

1. 状态定义：
   设 $dp[i][j][c][v]$ 表示到达第i行第j列时，持有c件宝贝且当前最大价值为v的方案数。

2. 状态转移方程：
   到达 $(i,j)$ 的方案数来自上方 $(i-1,j)$ 或左侧 $(i,j-1)$，分两种情况：

   • 不拿当前格子的宝贝：$$dp[i][j][c][v] += dp[\text{up/left}][c][v]$$
   • 拿当前格子的宝贝（需满足当前宝贝价值>v）：$$dp[i][j][c+1][\text{currentValue}] += dp[\text{up/left}][c][v]$$

3. 边界处理：

   • 当 $i=1$ 且 $j=1$（起点）：
     • 不拿：$dp[1][1][0][0] = 1$；
     • 拿：$dp[1][1][1][\text{起点价值}] = 1$；

4. 初始条件：

   • $dp[1][1][0][0] = 1$；（起点不拿宝贝的初始方案）
   • 其他状态初始值为0

5. 循环处理：

   • 遍历每个格子 $(i,j)$，再遍历当前持有宝贝数 $c$ 和最大价值 $v$，分别计算“不拿”和“拿”的方案数，累加至 $dp[i][j]$ 的对应状态；

6. 结果计算：
   统计 $dp[n][m][k][v]$ 的总和（v为所有可能的最大价值），即为恰好持有k件宝贝的方案数。

7. 复杂度：

   • 时间复杂度：$O(n \times m \times k \times V)$（V为宝贝价值的可能取值范围）；
   • 空间复杂度：$O(n \times m \times k \times V)$（可通过滚动数组优化空间）；